규도자 블로그
실패로부터 배우다 - 6. 퀀트 (페어트레이딩 편) 본문
이 사건을 이해하기 위해선 먼저 페어트레이딩이 무엇인지 알 필요가 있다. 페어트레이딩이라는 이름에서 유추할 수 있듯이 이 트레이딩방식은 가격 움직임의 유사성이 높은 두 종목간의 가격 오르내림을 이용하는 전략이다. 예를 들어 유사성이 높은 A주식과 B주식이 있는데 A주식은 오름세가 강해지고 있고 B주식은 내림세가 강해지고 있다손 치면 언젠가 이 A주식은 내리고 B주식은 오름으로써 평소의 유사도로 회귀한다는 '예상'을 갖고 A는 매도, B는 매수하는 것이 이 전략의 골자이다. 하지만 일반 주식현물은 매수 전에 먼저 매도계약을 가질 수 없기 때문에 전편에서 썼던 '주식선현물차익거래전략'에서 나오는 개별주식선물을 가진 종목들로만 할 수 있는 전략인 것이다.
내가 이 전략 알고리즘 매매 프로그램을 개발할 당시에는 주식과 ETF를 포함해 선현물 거래가 모두 가능한 종목은 총 151개였는데 지금은 몇 개인지 모르겠다. 그러니까 결국에 151개의 종목 각각을 또 150개와 비교하여(자기 자신 제외) 유사도가 높은 것들의 결과값을 보고 페어를 정하는게 이 전략의 첫번째 단계이다. 그러니까 약 10,000여개의 페어라는 경우의 수가 존재하니 이들의 유사도를 구하는 게 과제였는데 이를 어떻게 해결할까. 바로 야후 파이낸스가 해결해주었다.
야후 파이낸스에는 특정 주식의 2000년대부터 오늘까지의 하루단위 종가를 가격을 가져올 수 있다. 사실 개별주식선물에 올라와있던 151개 전부보다는 주로 KOSPI종목만 지원해서 KOSPI종목들로만 페어트레이딩 대상을 구성했었던 것 같다. 지금 다시 파일을 까보니 총 125종목이다. 아무튼 그렇게 2000년대부터 오늘까지의 하루단위 종가데이터를 가져와서 모든 경우의 수를 계산한 결과는 아래 파일과 같다.
파일을 업로드하려는데 게시글 쓰는 에디터에 파일업로드가 없어서 당황했다. 근데 그냥 드래그 앤 드롭하면 되는구나... 아무튼 유사도가 높은 것부터 내림차순으로 정렬했으니 어떤 종목이 유사도가 높은지 열자마자 확인할 수 있을 것이다. 파일이 열기 귀찮은 사람들을 위해 스크린샷으로 보여주자면

위와 같은 순서대로 주가가 유사한 움직임을 보여준다고 할 수 있다. 보통 이 페어트레이딩에서 페어를 구할 땐 유사해보이는 두 종목을 갖고 분석을 한다. 그러니까 반도체 2대장인 삼성전자와 하이닉스를 예로 들자면 둘 다 각분야의 대장주이고 업종이 비슷하니 비슷한 움직임을 가지지 않을까? 한번 분석해보자! 하는 생각으로 두 종목을 선정하고 가격을 가져와 분석하는 것이다. 선 선정, 후 분석이라고 할 수 있는데 보통 페어트레이딩에 대한 페어들을 찾을 땐 이렇게 비슷한 업종과 비슷한 규모를 가진 회사라던가 혹은 지주회사와 계열사라던가 하는 방법으로 찾는다. 하지만 난 이 많은 회사들을 일일히 비교하기 힘들고 굉장히 시간이 많이 걸린다는 생각을 갖고 있었기 때문에 이렇게 모든 데이터를 가져와서 결과값을 도출한 것이다.
아참, 위 결과값은 상관계수(correlation coefficient)를 이용해 도출한 결과값이다. 식은

이런 형태이다. 간단하게 구하는 방법이 있는데 모집단의 공분산을 모집단의 표준편차 곱하기 표본집단의 표준편차로 나누면 구해진다. 수학적으로도 얘기를 좀 풀어보려고 생각해보다가 이걸 풀려니정규화가격, 분산, 공분산, 공적분, 샤피값 등등 갑자기 정신이 혼미해진다. 그러니까 대충 수학적인 얘기는 여기서 끊고 저 위의 목록들 중 좋은 예를 하나 들어보자.
아, 일단 이 글을 보는 누군가가 내가 이 과정에서 구한 아웃풋을 구할 수도 있으니 파일로 업로드해두겠다. 확인해보니 3월 12일까지를 기준으로 한 페어트레이딩 리스트에 상관계수, 공적분계수, 스프레드 평균, 잔차가 포함된 엑셀파일이다.
예를 쉬운 예(삼성-하닉, 혹은 기아차-현대차)로 들려고 했는데 다시 만들긴 귀찮고 하니 예전에 만들어준 예제를 통해 위 전략의 방법과 실패방법 그 모두를 설명하겠다.

위 그래프는 더 위에 있는 페어트레이딩 리스트 2위에 랭크돼있던 0.973이상의 유사도를 보여준 현대해상과 DB손해보험의 20년간 일간 종가 정규화 가격 이동 그래프이다. 그림이 작아 보이지 않는다면 파란색이 현대해상, 주황색이 DB손해보험의 그래프라고 보면 된다.
아무튼 페어트레이딩이라는 전략의 시나리오대로라면 파란색이 위에 있을 땐 현대해상 매도, DB손보 매수를 하고 두 그래프가 교차되는 시점이 온다면 포지션을 청산하고, 다시 주황색이 위에 있을 땐 DB손보 매도, 현대해상 매수를 하고 두 그래프가 교차되는 시점이 온다면 포지션을 청산... 이런식으로 움직이는 것이다. 이것이 평균회귀를 신뢰하는 데서 착안한 페어트레이딩이라는 전략의 골자이다.
말로만 설명하면 참 쉽다. 전에 시도했던 선현물차익거래전략과는 달리 시간적인 민감함도 필요 없다. 하지만 보다 심플하고 간결한 문제가 있었다. 바로 '회전율'이 좋지 않다는 점이다. 심지어는 한국시장의 개별주식선물은 매월 두번째 목요일이 결제일이기 때문에 포지션을 청산하지 않는 이상 매월마다 롤오버비용이 월단위 고정비용으로 들어가게 된다.
자, 위의 그래프를 확대해서 구체적인 예를 들어보자.
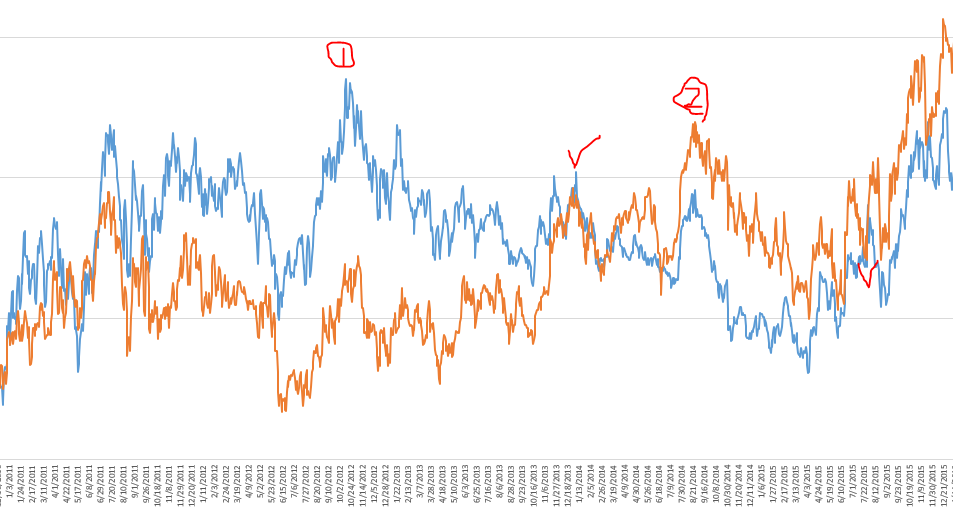
2011년부터 2015년까지의 정규화가격 그래프를 확대해봤다. 마찬가지로 파란색이 현대해상, 주황색이 DB손해보험이다. 이 케이스에서 베스트 시나리오라고 한다면 내가 터치패드로 꾸물꾸물 구려놓은 1번 시점에서 현대해상을 매도, DB손해보험을 매수하고 다음에 오는 체크포인트(정규화 가격 그래프가 겹치는 시점)에서 청산을 한 뒤에 2번 시점에서는 DB손해보험을 매도, 현대해상을 매수한 뒤에 다음 체크포인트에서 청산하면 된다.
글로는 정말 간단하면서도 완성돼있는 차트를 보면서 시나리오를 그려보면 너무나도 뻔한 흐름이지만 실제로 시장이 돌아가고 있는 동안은 1번시점이 제일 많이 벌어진 시점이라는 걸 유추하긴 쉽지 않다. 그러니까 결국 분할진입이 필요하다는 것이다. 분할진입의 기준은 공적분계수와 샤피를 이용하여 구한다손 쳐도... 물론 이것도 쉬운 알고리즘은 아니지만 그럼에도 불구하고 더 큰 문제가 남아있다. 위에서도 말했던 롤오버 비용이다. 베스트 시나리오라고 생각했던 1번진입후 청산, 2번진입후 청산하는 이 과정은 약 16개월(1번 진입후 청산) + 12개월(2번 진입후 청산), 총 28개월의 기간이 걸린다. 예를 든 이 케이스 말고도 20년짜리 페어 트레이딩 그래프를 보면 알겠지만 한 번의 진입과 청산에 못해도 몇 개월씩은 걸린다. 이 개월개월이 전부 비용이라는 것이다. 정말 우연에 우연의 일치가 계속돼 롤오버를 해야하는 시점마다 완벽한 조건의 호가가 존재한다고 해도 롤오버 한번의 총 투자금액의 0.012%가 계속 소비된다. 이게 1년이면 0.144%가 된다. 그럼에도 불구하고 이 페어트레이딩 전략이란 장기간에 걸쳐 적게는 몇 퍼센트, 많게는 수십 퍼센트의 이익을 얻을 수 있으니 감수할만하지 않냐고 하겠지만 이건 말 그대로 우연에 우연의 일치를 더한 것이다. 실제 돌아가는 시장에 대입해보면 베스트 케이스라고 해봤자 롤오버할 때마다 상대가에서 1호가 불리하게 체결된다. 전편에서 말했듯이 1,000원짜리 주식이라면 5원, 100,000원짜리 주식이라면 50원, 뭐 이런 식 말이다. 매도계약을 들고 있다면 매도계약의 상대가인 매수계약은 분명 매도계약보다 저렴하게 형성돼있는데 그 가격으로 처분할 수밖에 없고, 매수계약을 들고 있다면 그 반대가 된다. 1000원에 체결한 주식선물의 매수계약을 예로 들자면 현재 매도1호가가 995원일 때 청산하여 5원의 손해를 보고, 995원이 매도1호가이면 호가창이 타이트하게 구성돼있다는 가정 하에 매수1호가는 990원일 것이므로 그 가격으로 새 계약을 체결해야 한다. 매도계약 또한 마찬가지이다. 결제일이 다가오면 다가올수록 주식 현물의 가격과 비슷해지므로 호가창 또한 비슷한 흐름을 보이는데 보통 이런 흐름이라고 보면 된다. 아무튼 중요한 건 주식선물을 보유하는 것 자체가 리스크라는 것이다. 그리고 실제로 프로그램으로 돌리고 있었다면 1번시점 뿐만 아니라 1번으로 다가가는 시점에 계속해서 계약들을 쌓아나갔을 것이기 때문에 롤오버를 하게 될수록 불리한 가격으로 체결을 하기 때문에 손해가 극심해진다. 수수료 + 상대가 체결에 의한 손해가 이 전략의 리스크이다.
그리고 추가로 주식선물엔 multiplier개념이 있는데 1계약이 주식 10개의 가치를 갖고 있고 뭐 그런 거다. 한국용어로는 '승수'라고 한다. 그러니까 간단하게 말하자면 주식선물은 한번에 주식을 10개씩 사거나 팔아야 한다는 얘기다. 이렇게 커다란 뭉치로 거래되는 주식선물을 정규화된 가격으로 두개의 페어 모두 똑같은 가치를 지닌 양만큼 계약을 체결한다면 과연 그 비용이 얼마나 될까. 예를 들어 A주식은 10,000원이고 B주식은 1,000원이라면 A주식의 선물은 1계약당 100,000원이 되고 B주식의 선물은 1계약당 10,000원이 되는데 이 두 주식을 똑같은 가치만큼 갖고 있어야 가격이 오르내릴 때마다 그 차액만큼의 이득을 얻을 수 있을 것 아닌가. 결국 이 둘의 notion을 맞추려면 A주식의 선물 1계약당 B주식의 선물 10계약을 들고 있어야 한다.
하지만 보통 이렇게 완벽히 10배의 가격을 가진 종목끼리 페어가 될리 만무하지 않은가. 간단하게 하이닉스와 삼성전자를 예로 들자면 글을 쓰고 있는 현재 삼성전자의 종가는 79,900원이고 하이닉스의 종가는 121,500원이다. 그렇다면 삼성전자 선물의 1계약은 799,000원, 하이닉스 선물의 1계약은 1,215,000원이 될 것이다. 하지만 이렇게 단순히 1계약씩 하면 두 종목 사이의 차액인 416,000원이라는 델타가 뜨게 된다. 이는 총 notion금액인 2,014,000원의 20%에 해당하는 큰 금액이다. 그러니까 결국 삼성전자 3계약으로 2,397000원을 삼성전자 선물에, 하이닉스 2계약으로 2,430,000원을 하이닉스 선물에 투자해야지만 어느정도 두 종목 사이의 괴리를 줄일 수 있게 되는 것이다. 이렇게 하면 차액은 33,000원으로서 notional의 0.68%에 해당하는 합리적인 델타만 남는다. 물론 이 과정은 시장의 변동에 따라서 계속해서 비율이 달라진다. 당장 내일 삼성이 6만원 되고 하이닉스가 12만원이 된다고 치면 위에서 예를 든 것처럼 3:2계약이 아닌 2:1계약을 해야 한다.
그러니까 정리하자면 너무나도 큰 금액이 필요하고, 롤오버비용이 상당하고, 한 번의 청산까지 엄청나게 오래걸린다는 것 때문에 페어트레이딩 전략 또한 무위로 돌아갔다. 이것을 계기로 주식시장에서의 퀀트전략은 접게 된다... 그렇다면 다음은? 바로 암호화폐시장 퀀트이다. (물론 망했다)
'시행착오 > 실패로부터 배우다' 카테고리의 다른 글
| 실패로부터 배우다 - 7. 完: 실패는 실패다 (3) | 2021.07.10 |
|---|---|
| 실패로부터 배우다 - 6. 퀀트 (암호화폐 편) (0) | 2021.07.08 |
| 실패로부터 배우다 - 6. 퀀트 (주식 선현물차익거래 편) (0) | 2021.07.07 |
| 실패로부터 배우다 - 5. 유튜버 (0) | 2021.07.04 |
| 실패로부터 배우다 - 4. 이스코어드닷컴 (0) | 2021.07.04 |

