재귀함수로 구하는 피보나치 수열의 직관성

재귀함수로 구하는 피보나치 수열의 직관성

나는 항상

def fib(n):
    head, body, tail = 0, 1, 0

    for _ in range(n):
        tail = head + body
        head = body
        body = tail
    return head

Python

Copy

이런식으로 피보나치 수열의 몇 번째 수를 구하곤 했었다. 연산도 빠르고 코드도 직관적이라서 피보나치수열을 응용해야하는 문제가 있을 때마다 항상 이 로직을 애용해왔는데 얼마 전에 피보나치수열을 재귀로 구현해야했다. 하지만 이 로직에 뇌가 절여진 나는 구현하지 못했다. 아, 참고로 피보나치수열을 재귀로 구하는 방법은

def fib(n):
    if n == 0:
        return 0
    elif n == 1 or n == 2:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

Python

Copy

위와 같다. 먼저 썼던 함수와 이 함수는 같은 결과를 리턴한다.

 

이 재귀 함수는 내가 구현한 것이 아니라 인터넷에 널리 퍼져있는 것을 긁어온 것이다. 왜냐. 위에서 말했듯이 난 꽤 오랜 시간동안 "피보나치수열의 n번째 수에 대한 함수를 리턴하는 재귀함수"를 로직으로 구현해낼 수 없었기 때문에. 그리고 심지어는 완성된 함수를 보고서도 "이게 왜 피보나치 수열의 n번째 수를 리턴할까?" 고민했다. 그 과정은 종이에 그려보니까 이해가 되더라.

 

말로 단순히 설명하면 위 함수는 "n이라는 숫자를 넣었을 때 함수가 전부 진행되고 나면 1과 2의 갯수가 총 몇개가 나오는가"에 대한 결과를 알려주는 함수이다.

 

5를 넣었을 땐 이렇게 진행된다.

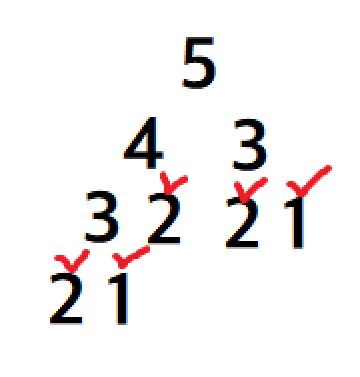
함수를 돌린 결과 2와 1이 총 5개가 나온다. 그래서 피보나치수열의 5번째 숫자는 5가 되는 것이다.

 

그렇다면 6은?

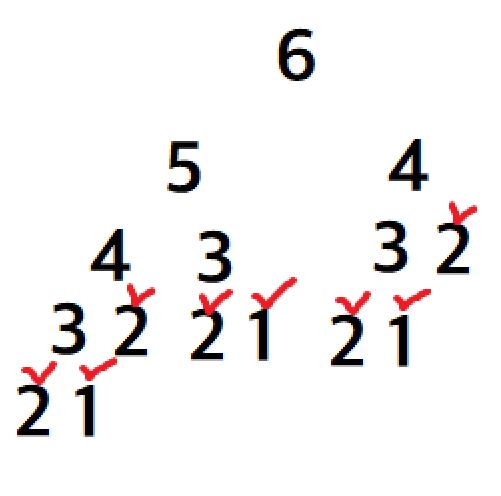
함수를 돌린 결과 2와 1이 총 8개가 나온다. 그래서 피보나치 수열의 6번째 숫자는 8이 되는 것이다.

 

이제 좀 감이 올 것이다. n이 5일땐 n이 4일때의 삼각형과 3일때의 삼각형이 합쳐진 모양이고 6일땐 5삼각형과 4삼각형이 각각 합쳐진 모양이다. 각 삼각형을 해당 숫자가 들어갔을 때의 결과값으로 치환해보면 f(6)일땐 f(5) + f(4), f(5)일땐 f(4)와 f(3)... 이렇게 반복되며 결국 피보나치 수열의 진행과 같은 결과값을 내뱉는 것이다.

 

오랜만에 재밌는 문제였다.

• 카카오스토리
• 트위터
• 페이스북

'알고리즘 > 개념' 카테고리의 다른 글

재귀함수로 구하는 피보나치 수열의 직관성에 대하여  (0)	2021.10.28
에라토스테네스의 체 (소수구하기. 파이썬)  (0)	2021.04.19
최대공약수(Greatest Common Divisor)와 최소공배수(Least Common Multiple) 구하기 - 파이썬3  (0)	2021.03.31
피즈버즈 테스트(FizzBuzz Test) - 파이썬3(python3)  (0)	2019.02.12